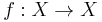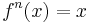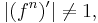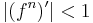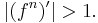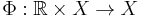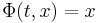Periodic point

In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.

1 Iterated functions
- 1.1 Examples
2 Dynamical system
- 2.1 Properties
3 See also

Iterated functions

Given an endomorphism f on a set X

$f: X \to X$

a point x in X is called periodic point if there exists an n so that

$\ f^n(x) = x$

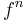where $f^n$ is the nth iterate of f. The smallest positive integer n satisfying the above is called the prime period or least period of the point x. If every point in X is a periodic point with the same period n, then f is called periodic with period n.

If f is a diffeomorphism of a differentiable manifold, so that the derivative 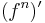$(f^n)^\prime$ is defined, then one says that a periodic point is hyperbolic if

$|(f^n)^\prime|\ne 1,$

and that it is attractive if

$|(f^n)^\prime|< 1$

and it is repelling if

$|(f^n)^\prime|> 1.$

If the dimension of the stable manifold of a periodic point or fixed point is zero, the point is called a source; if the dimension of its unstable manifold is zero, it is called a sink; and if both the stable and unstable manifold have nonzero dimension, it is called a saddle or saddle point.

Examples

A period-one point is called a fixed point.

Dynamical system

Given a real global dynamical system (R, X, Φ) with X the phase space and Φ the evolution function,

$\Phi: \mathbb{R} \times X \to X$

a point x in X is called periodic with period t if there exists a t ≥ 0 so that

$\Phi(t, x) = x\,$

The smallest positive t with this property is called prime period of the point x.

Properties

Given a periodic point x with period t, then 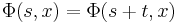$\Phi(s, x) = \Phi(s %2B t, x)\,$ for all s in R
Given a periodic point x then all points on the orbit 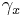$\gamma_x$ through x are periodic with the same prime period.

Periodic point

Contents

Iterated functions

Examples

Dynamical system

Properties

See also